Bayes rule

This week, we will apply Bayes rule to a simple exercise, which will be introduced in class. Below you find useful R syntax that will help you code the exercise.

Bayes rule (in discrete form) is:

\[\Pr(H_j|D)=\frac{\Pr(D|H_j)\cdot\Pr(H_j)}{\sum_{j=1}^{k}\Pr(D|H_j)\cdot\Pr(H_j)}\]

\(\Pr(H_j|D)\) is the posterior probability, i.e. the probability of hypothesis \(H_j\) given the data (evidence) \(D\) at hand.

\(\Pr(H_j)\) is the prior probability, i.e. the probability of hypothesis \(H_j\) before we have seen (unconditional on) any data.

\(\Pr(D|H_j)\) is the likelihood of data \(D\) given hypothesis \(H_j\). This is our model of the data generation process under the hypothesis. The likelihood updates the prior to the posterior.

\(\sum_{j=1}^{k}\Pr(D|H_j)\cdot\Pr(H_j)\) is the total probability of the data, summing over all \(k\) hypotheses. It serves to normalise the numerator in Bayes rule so that the posterior distribution over all hypotheses has an integral of \(1\) and is thus a probability distribution.

Useful syntax

You might find this R syntax helpful when coding the exercise.

Defining an array:

# array of discrete numbers
x <- c(1, 2, 3, 4)
x
## [1] 1 2 3 4
# array of sequence of numbers between two bounds with a certain increment
y <- seq(from = 0, to = 10, by = 1)
y
##  [1]  0  1  2  3  4  5  6  7  8  9 10

Calculating values of a probability distribution/density function at certain locations of the distribution:

# uniform distribution between 0 and 10 for sequence y
du <- dunif(y, min = 0, max = 10)
plot(y, du)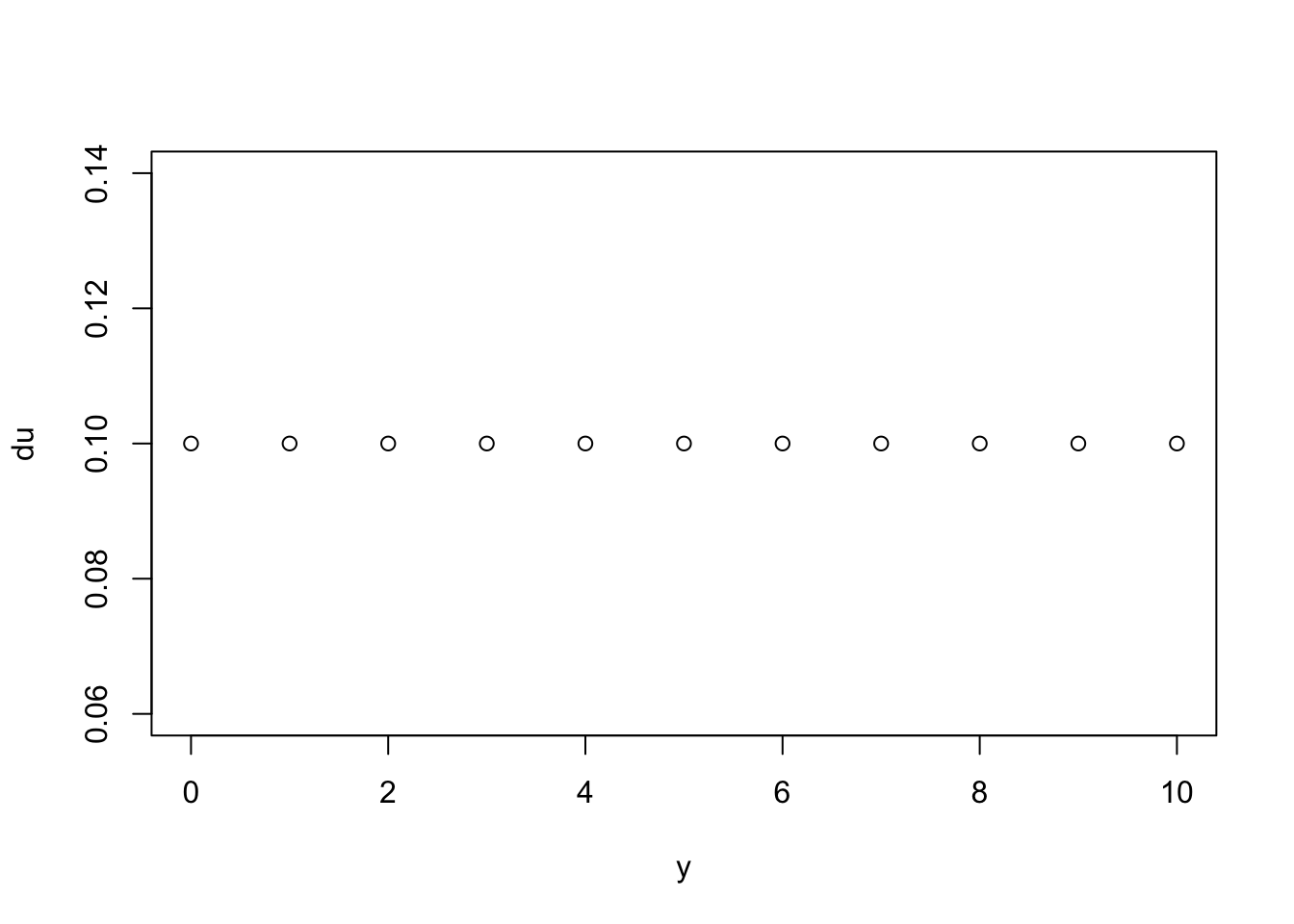

# normal distribution N(5,1) for sequence y
dn <- dnorm(y, mean = 5, sd = 1)
plot(y, dn)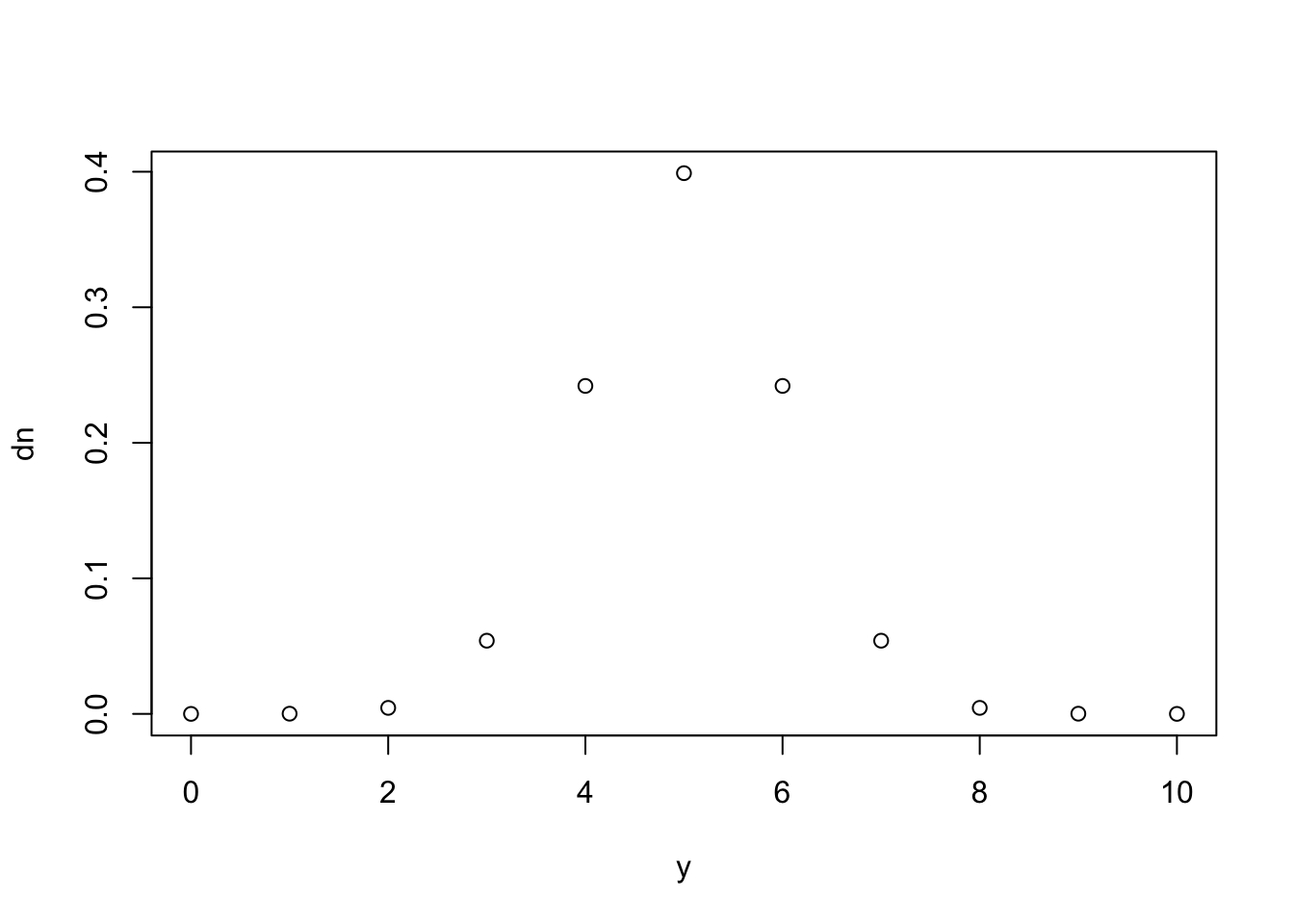

Other distributions can be accessed the same way: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Distributions.html.

Sampling from an array with a certain probability of obtaining each element:

# here sampling 1000 times
s <- sample(y, size = 1000, replace = TRUE, prob = dn)
hist(s)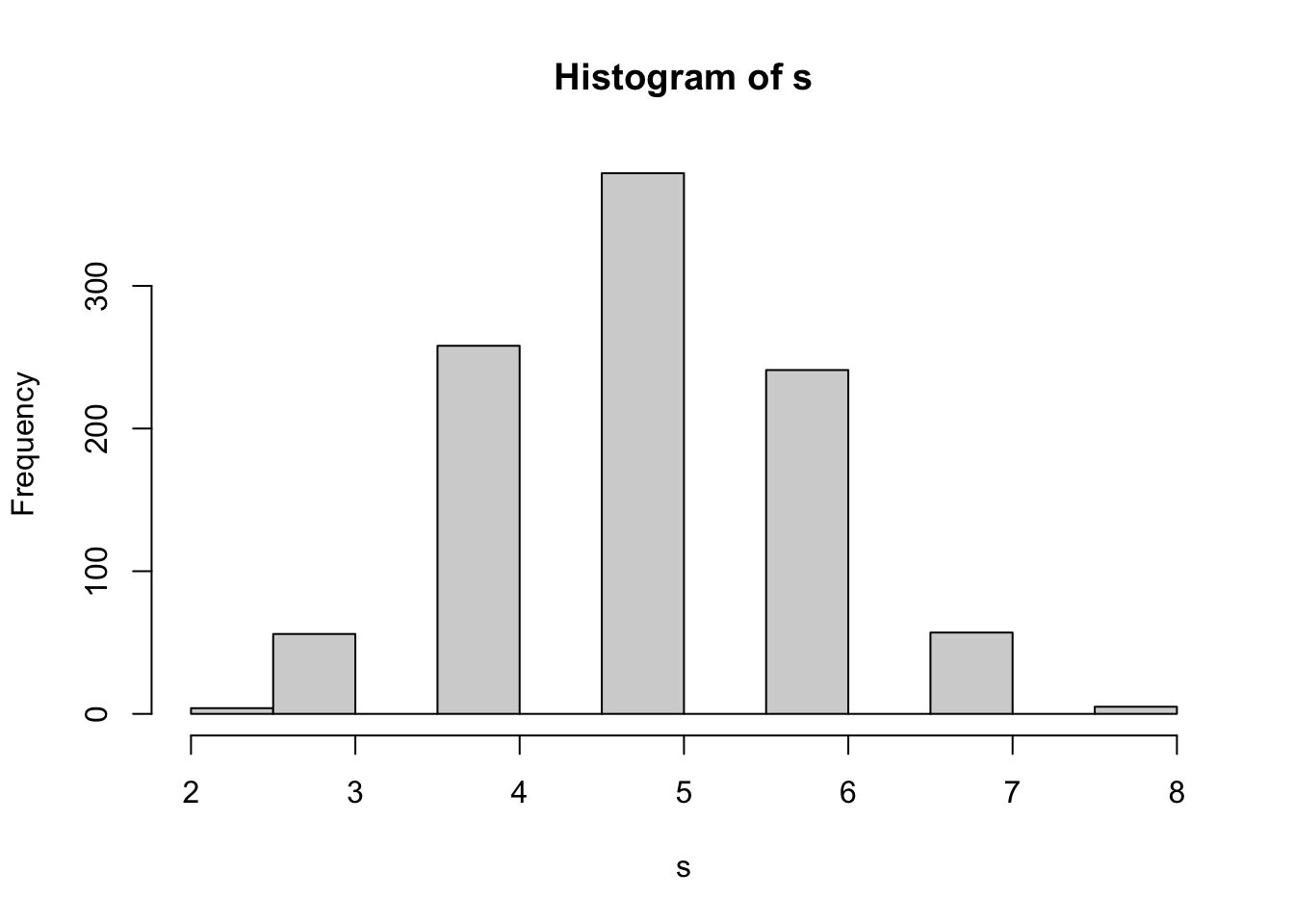


Copyright © 2024 Humboldt-Universität zu Berlin. Department of Geography.