Content

  • Log-linear regression: count response data (Poisson model with log-link)
  • Over-dispersion: quasi-Poisson model
  • Over-dispersion: negative-binomial model

Poisson model

The following data set shows bird counts over a topographic relief gradient:

dat <- read.table("Data/bird_counts.txt", sep = ";", header = TRUE)
head(dat)
##   relief   Y
## 1  0.576 129
## 2  0.576 166
## 3  0.576 137
## 4  0.576 105
## 5  0.576 155
## 6  0.576 178
ggplot(dat, aes(x = relief, y = Y)) + 
  geom_point()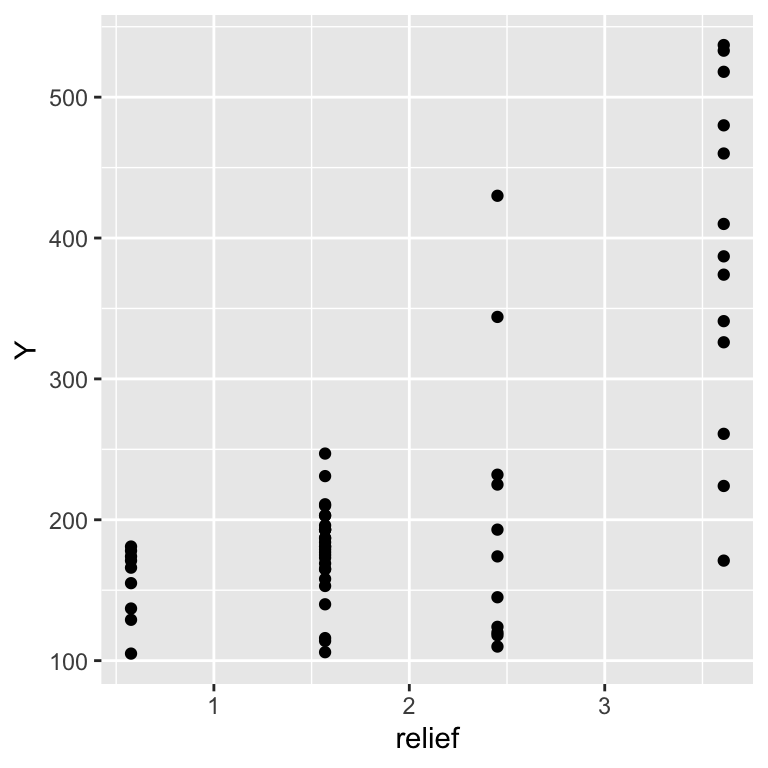

ggplot(dat, aes(x = relief, y = Y)) + scale_y_continuous(trans='log') +
  geom_point()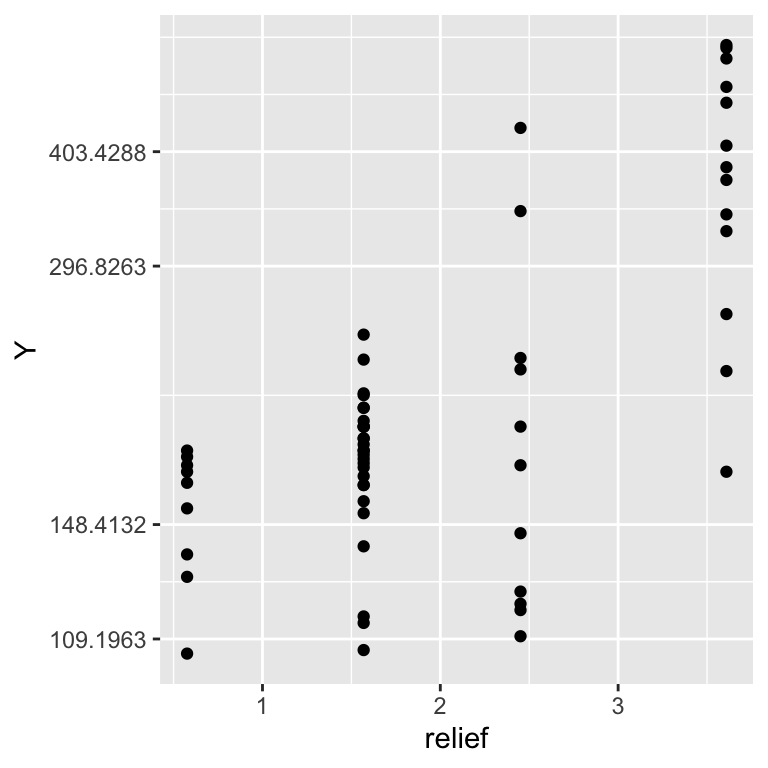

The data is bounded to positive values, a log-link is thus recommended:

\(counts_{expected} = log^{-1}(\beta_0 + \beta_1 * relief) = exp(\beta_0 + \beta_1 * relief)\)

As the data can only take natural numbers (0, 1, 2, …), we need a discrete response distribution. For count data, the Poisson distribution is a good choice, yielding the final model of:

\(counts \sim Poisson(exp(\beta_0 + \beta_1 * relief))\)

bird.poisson <- glm(Y ~ relief, data = dat, family = poisson(link = "log"))
summary(bird.poisson) 
## 
## Call:
## glm(formula = Y ~ relief, family = poisson(link = "log"), data = dat)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) 4.665888   0.021577  216.24   <2e-16 ***
## relief      0.339559   0.008382   40.51   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 2921.1  on 60  degrees of freedom
## Residual deviance: 1299.6  on 59  degrees of freedom
## AIC: 1739.7
## 
## Number of Fisher Scoring iterations: 4

Dispersion

  • Dispersion quantifies, how much higher (or lower) the observed variance is relative to the expected variance of the model.

  • For the Poisson distribution, the expected value is equal to the variance, i.e. the variance increases 1:1 with the mean value. Hence, dispersion = 1.

  • In other words, when we fit a Poisson model, we expect the variance to increase with the mean value by a factor of 1.

  • If the variance decreases at a lower rate, then the data are under-dispersed

  • If the variance decreases at a higher rate, then the data are over-dispersed. This is often the case.

Consequences of over-dispersion

With a correct mean model we have consistent estimates of the parameters but over-dispersion leads to:

  • underestimation of the standard errors of the parameter estimates

  • selection of overly complex models

Over-dispersion

To get a rough estimate on over-dispersion, divide the residual deviance by the residual degree’s of freedom. The ratio should be below 1. Values much larger (> 2) indicate over-dispersion (or under-dispersion if less than 0.6).

## Residual deviance: 1299.6  on 59  degrees of freedom
summary(bird.poisson)$deviance / summary(bird.poisson)$df.residual
## [1] 22.02709

Our model appears to be over-dispersed, indicating:

  1. bad model fit (omitted terms/variables, incorrect relationship/link, outliers)

  2. the variation of Y is greater than predicted by the model

Remedy:

  1. Change distribution/link-function

  2. Change optimization (quasi-likelihood)

quasi-Poisson model

In the quasi-poisson regression, the variance is assumed to be a linear function of the mean.

bird.quasip <- glm(Y ~ relief, data = dat, family = quasipoisson)
summary(bird.quasip) 
## 
## Call:
## glm(formula = Y ~ relief, family = quasipoisson, data = dat)
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.66589    0.09953  46.878  < 2e-16 ***
## relief       0.33956    0.03866   8.782 2.64e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 21.27853)
## 
##     Null deviance: 2921.1  on 60  degrees of freedom
## Residual deviance: 1299.6  on 59  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 4

negative-binomial model

In the negative-binomial regression, the variance is assumed to be a quadratic function of the mean, modulated by an additional variance parameter.

library(MASS)
## 
## Attaching package: 'MASS'
## The following object is masked from 'package:dplyr':
## 
##     select
bird.nb <- glm.nb(Y ~ relief, data = dat, link = log)
summary(bird.nb) 
## 
## Call:
## glm.nb(formula = Y ~ relief, data = dat, link = log, init.theta = 11.71533906)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.72453    0.08796  53.714  < 2e-16 ***
## relief       0.31269    0.03893   8.032 9.59e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(11.7153) family taken to be 1)
## 
##     Null deviance: 134.313  on 60  degrees of freedom
## Residual deviance:  61.519  on 59  degrees of freedom
## AIC: 681.88
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  11.72 
##           Std. Err.:  2.21 
## 
##  2 x log-likelihood:  -675.879

Parameter estimates

The coefficients of all above models can be interpreted easily, as the coefficients are multiplicative when back-transformed to the response (count) scale. That is, with a one unit increase in x, the count is multiplied by the exponential of the coefficient. For our example, we expect a 1.4 times (or 40%) increase in mean bird counts with a one unit increase in relief. You can use confint() to compute confidence intervals for the parameters.

# Poisson
coeffs <- exp(coef(bird.poisson))
coeffs_ci <- exp(confint(bird.poisson))
cbind(coeffs, coeffs_ci) 
##                 coeffs      2.5 %     97.5 %
## (Intercept) 106.259866 101.846790 110.836066
## relief        1.404328   1.381446   1.427589
# quasi-Poisson
coeffs <- exp(coef(bird.quasip))
coeffs_ci <- exp(confint(bird.quasip))
cbind(coeffs, coeffs_ci)
##                 coeffs     2.5 %     97.5 %
## (Intercept) 106.259866 87.187307 128.808562
## relief        1.404328  1.301813   1.514927
# negative-binomial
coeffs <- exp(coef(bird.nb))
coeffs_ci <- exp(confint(bird.nb))
cbind(coeffs, coeffs_ci) 
##                 coeffs     2.5 %     97.5 %
## (Intercept) 112.677003 95.549671 133.298947
## relief        1.367104  1.271319   1.471155

\(\text{pseudo-}r^2\)

\(\text{pseudo-}r^2 = 1-\frac{\text{residual deviance}}{\text{Null deviance}}\)

pseudo_r2 <- 1 - bird.quasip$deviance / bird.quasip$null.deviance
pseudo_r2
## [1] 0.5551062

Plot model with effects package

efct <- effect("relief", mod = bird.quasip, xlevels = list(relief = seq(0, 4, length.out = 100)))
efct <- as.data.frame(efct)

p <- ggplot() +
  geom_point(data = dat, aes(x = relief, y = Y)) +
  geom_ribbon(data = efct, aes(x = relief, ymin = lower, ymax = upper), alpha = 0.3) +
  geom_line(data = efct, aes(x = relief, y = fit))
print(p)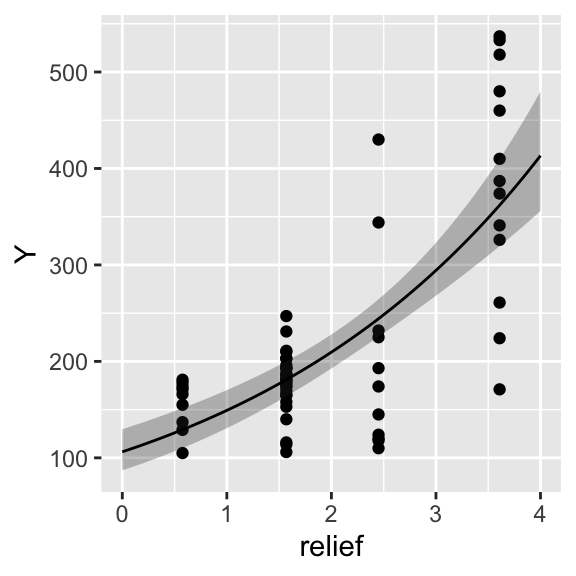

Plot fitted values with ggplot

library(gridExtra)
plot1 <- ggplot(dat, aes(x = relief, y = Y)) + 
                geom_point() + 
                geom_smooth(method = "glm", method.args=list(family = "poisson"), col = "red") 

plot2 <- ggplot(dat, aes(x = relief, y = Y)) + 
                geom_point() + 
                geom_smooth(method = "glm", method.args=list(family = "quasipoisson"), col = "red")

grid.arrange(plot1, plot2, ncol = 2)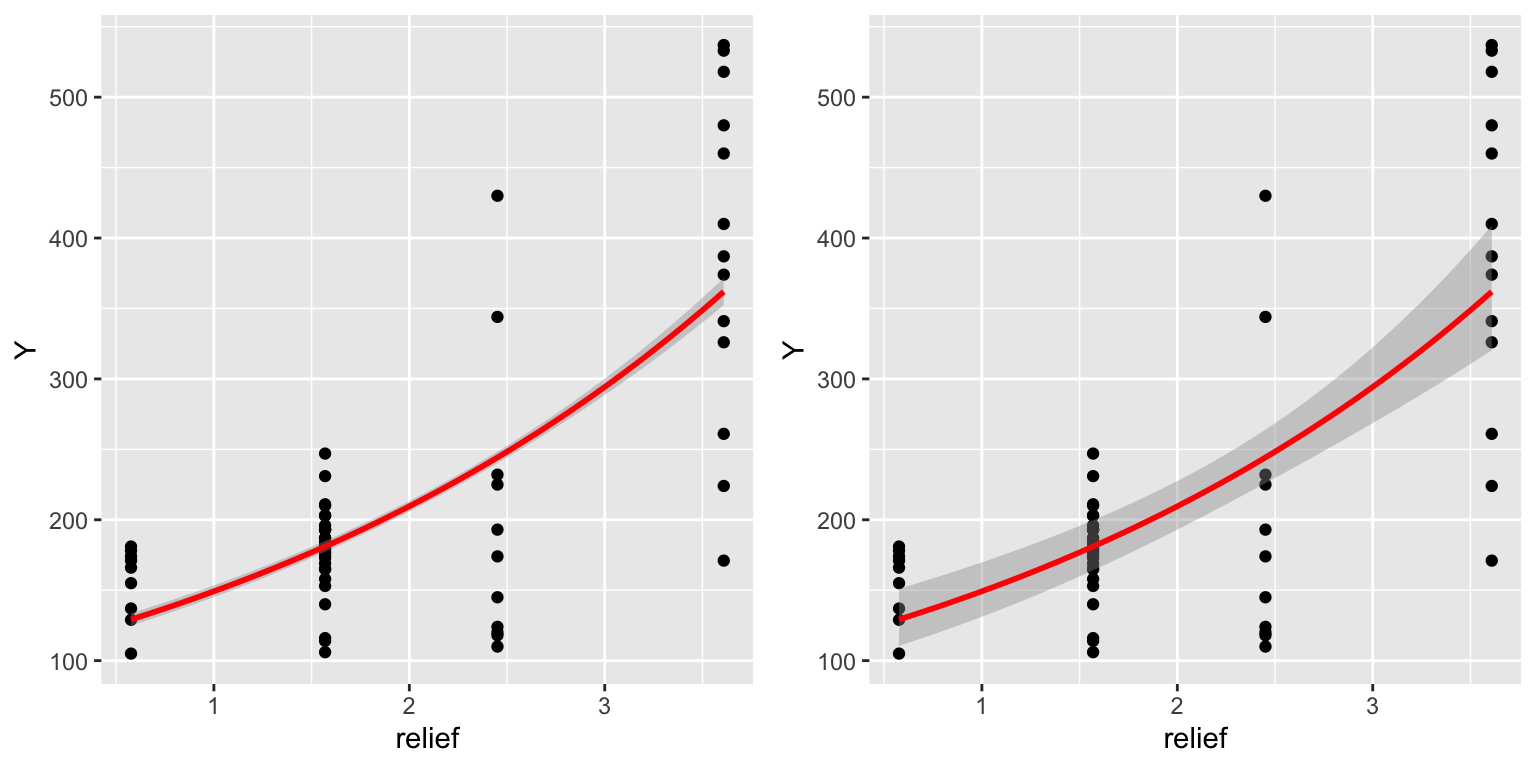

plot3 <- ggplot(dat, aes(x = relief, y = Y)) + 
                geom_point() + 
                geom_smooth(method = "glm.nb", method.args=list(link = "log"), col = "red")

grid.arrange(plot1, plot2, plot3, ncol = 3)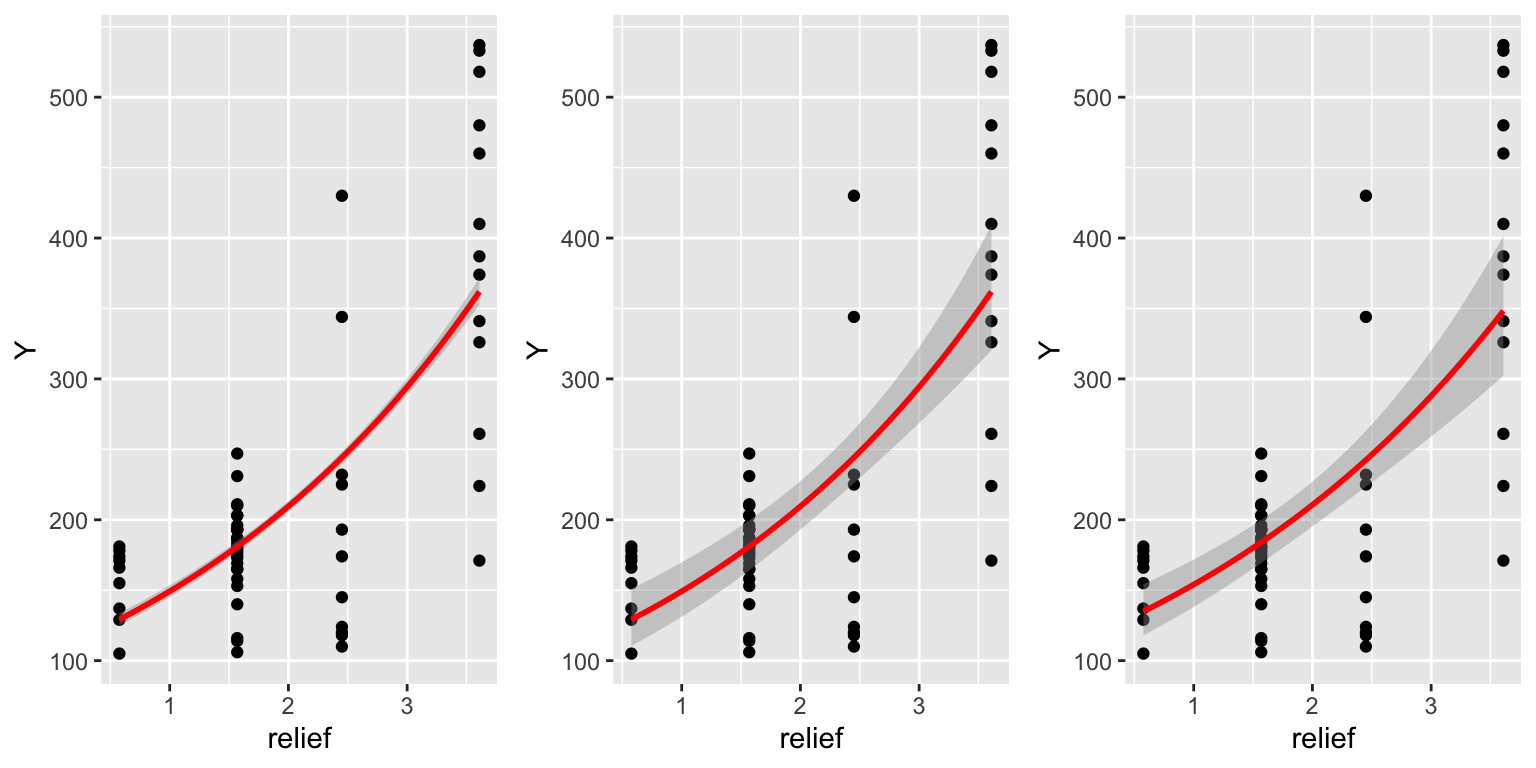


Copyright © 2024 Humboldt-Universität zu Berlin. Department of Geography.