Data

WorldClim is a database of high spatial resolution global weather and climate data that can be used for mapping and spatial modeling. The bioclim dataset dervies from worldclim, i.e., from monthly temperature and rainfall values to generate more biologically meaningful variables. Bioclim are often used in species distribution modeling and related ecological modeling techniques. The original bioclim dataset contains 19 layers. For this demonstration, we’ll use a random sample collected over a geographic subset and only a subset of the variables:

BIO1 = Annual Mean Temperature
BIO5 = Max Temperature of Warmest Month
BIO6 = Min Temperature of Coldest Month
BIO12 = Annual Precipitation

clim <- read.csv("Data/bioclim_subset_sample.csv")
head(clim)

##       Tmean     Tmax      Tmin   Precip
## 1  8.483958 21.75500 -7.096000 705.5000
## 2  6.497375 20.52900 -9.607000 749.0000
## 3 10.452375 24.45300 -5.697000 660.5000
## 4  8.237074 22.02089 -8.008889 637.1111
## 5  8.276444 21.41000 -6.908667 621.8333
## 6 11.461416 25.75200 -4.883000 684.2500

A look at the scatter plot matrix shows that Tmean and Tmax are strongly correlated with each other and that both variables are also correlated to some degree with Tmin. If we were to use these four variables in a regression model, we would face the issue of multicollinearity. Statistical inference for regression models hat contain intercorrelations among two or more independent variables is less reliable as multicolinearity leads to wider confidence intervals. In this case, it will likely be difficult to tell whether an effect is due to Tmean or Tmax. One way to reduce multicollinearity is to eliminate variables based on correlation coefficients or scientific knowledge. Often this is an effective approach if there is prior knowledge regarding the variables, but it can be cumbersome for larger sets of predictors. Another approach is the principal component analysis, which reduces the dimensionality (less predictors are needed) and it yields uncorrelated predictors.

pairs(clim)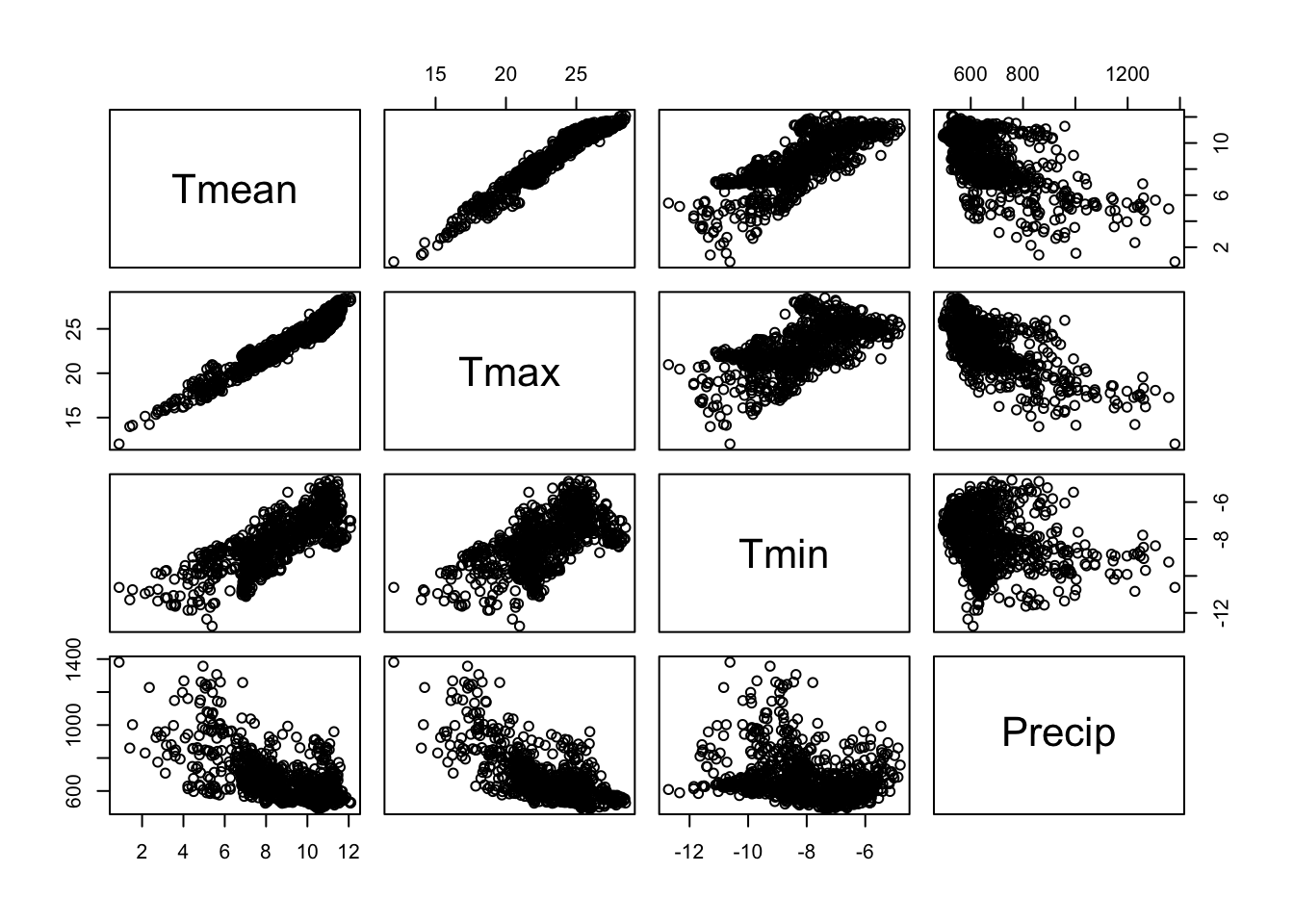

Fit PCA

There are two functions in R for performing a PCA: princomp() and prcomp(). While the former function calculates the eigenvalue on the correlation/co-variance matrix using the function eigen(), the latter function uses singular value decomposition, which numerically more stable. We here are going to use prcomp().

pca <- prcomp(clim, scale. = TRUE)

You should set the scale. argument to TRUE, to scale the data matrix to unit variances. The default is scale. = FALSE. You may also use scale() to standardize the original data matrix and then enter the standardized data matrix to prcomp.

Scores

The prcomp object stores the transformation and the transformed values, which are called scores. You can access the transformed dataset as follows:

pca_scores <- data.frame(pca$x)
head(pca_scores)

##           PC1        PC2        PC3         PC4
## 1 -0.10437038 -0.6623921  0.5218369 -0.06333806
## 2 -1.81424024  0.2309886 -0.1090850  0.02493079
## 3  1.57278761 -1.0321770  0.4015154  0.02441915
## 4 -0.19815948  0.1256635  0.3803971 -0.05908909
## 5  0.06685627 -0.2714205  1.0023861 -0.04971012
## 6  2.30800977 -1.5264628  0.2270009  0.07219499

You see the transformed variables (now called PC1, PC2, PC3, PC4) are uncorrelated.

pairs(pca_scores)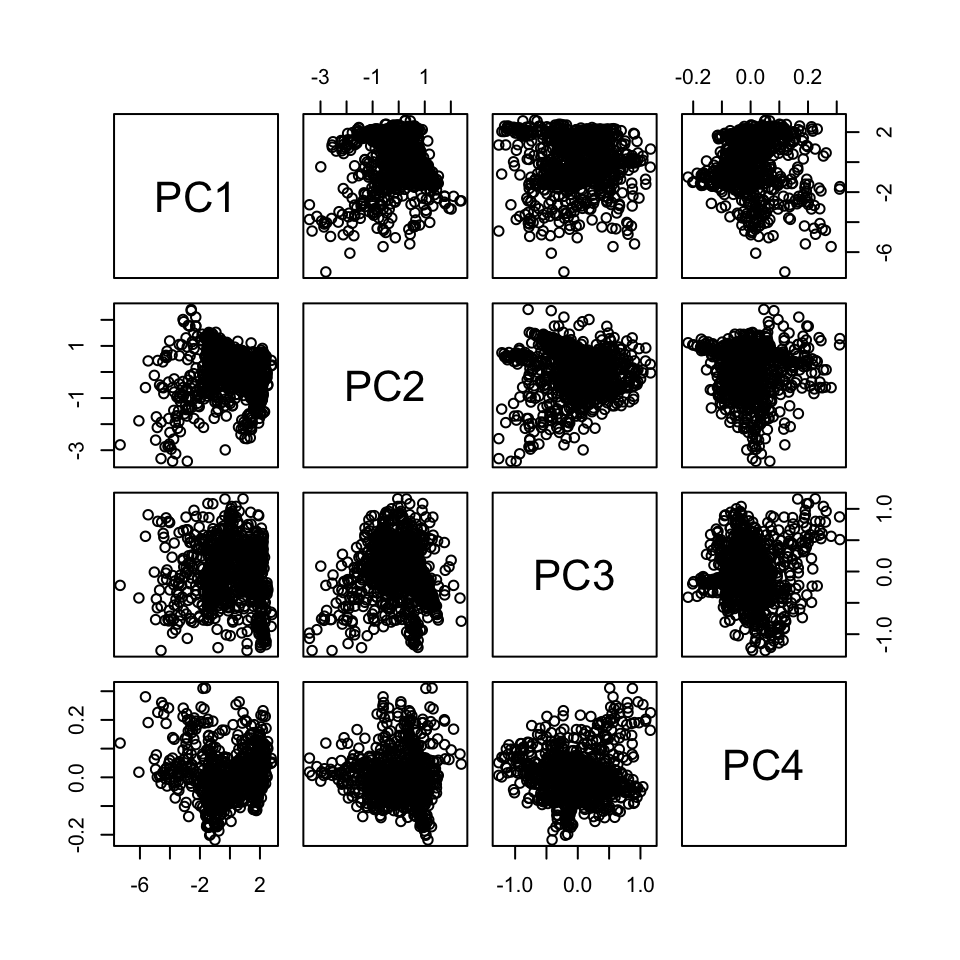

You can apply the transformation (rotation coefficients) to a dataset using the predict function. In the example below, the transformation is applied to the same dataset that was used to fit the transformation. Hence, the results are the same as the scores stored in the prcomp object (pca$x).

predicted_pca_scores <- predict(pca, clim)
head(predicted_pca_scores)

##              PC1        PC2        PC3         PC4
## [1,] -0.10437038 -0.6623921  0.5218369 -0.06333806
## [2,] -1.81424024  0.2309886 -0.1090850  0.02493079
## [3,]  1.57278761 -1.0321770  0.4015154  0.02441915
## [4,] -0.19815948  0.1256635  0.3803971 -0.05908909
## [5,]  0.06685627 -0.2714205  1.0023861 -0.04971012
## [6,]  2.30800977 -1.5264628  0.2270009  0.07219499

Rotation coefficients

The PCA transformation consists of rotation coefficients (eigenvectors). You can access the rotation coefficients stored in a prcomp object as follows:

pca$rotation

##               PC1        PC2        PC3         PC4
## Tmean   0.5671218 -0.1334564 -0.2842325 -0.76142902
## Tmax    0.5561077  0.0899659 -0.5600202  0.60747649
## Tmin    0.4561343 -0.6196440  0.5977105  0.22522181
## Precip -0.4013209 -0.7682036 -0.4983286  0.02175513

Recall, the coefficients describe how each PC is a linear combination of the input variables. An interesting analogy is a cooking recipe. The cooking recipe below defines the fractions of the climate variables that are needed (and added up) to “cook up” the first principle component.

\[PC1 = 0.567 * Tmean + 0.556 * Tmax + 0.456 * Tmin + -0.401 *Precip\] Let’s do this calculation for the first observation in our bioclim dataset. Note, that below I scale the variables to unit variance and mean zero (z-score). When running the principal component analysis above, I set the scale argument of the prcomp function to TRUE, which has the same effect.

# first observation
clim_obs <- head(scale(clim),1)
clim_obs

##            Tmean       Tmax      Tmin    Precip
## [1,] -0.07088585 -0.4483495 0.6604827 0.2893138

# rotation coefficients of the first PC
pca1_coeff <- pca$rotation[,1]
pca1_coeff

##      Tmean       Tmax       Tmin     Precip 
##  0.5671218  0.5561077  0.4561343 -0.4013209

Multiplying the observation vector and the coefficient vector is a vectorized operation. That is, the first element of the first vector is multiplied with the first element of the second vector, the second element of the first vector is multiplied with the second element of the second vector, etc.

sum(clim_obs * pca1_coeff)

## [1] -0.1043704

We just calculated the score of the first principle component (PC1) for a single observation. The PC1 is a transformation (the cooking recipe) and the score is the value you get when applying the transformation. Let’s compare our score with the one obtained with prcomp.

head(pca$x, 1)

##             PC1        PC2       PC3         PC4
## [1,] -0.1043704 -0.6623921 0.5218369 -0.06333806

So, the coefficients reflect the contribution of each variable to each principal component. For example, the absolute magnitude of the $PC1$ coefficients for $Tmean$, $Tmax$, $Tmin$, and $Precip$ is relatively similar, which indicates that all four variables contribute (roughly) similarly to PC1.

The sign of the coefficients tells us something about the direction, i.e., $PC1$ increases with increasing $Tmean$, $Tmax$, and $Tmin$, whereas $PC1$ decreases with increasing $Precip$. Note, however, the direction of the eigenvector is arbitrary. The equation below flips the signs of the coefficients (direction of the eigenvector). The inverse: $-1 * PC1$ is equally valid:

\[PC_i \hat{=} -PC_i\]

So, do not get attached to the direction of the PC1. But what the signs tell us is: $Tmean$, $Tmax$, and $Tmin$ have an opposite sign to $Precip$. We can also say: $Tmean$, $Tmax$, and $Tmin$ form a contrast to $Precip$ (while one has a positive effect the other has a negative effect or vice versa). Now, to interpret what that means requires scientific knowledge of the underlying ecological, climatological, biological, or socio-ecological gradients you might be observing here, e.g. elevation gradients, continentality, etc.

Eigenvalues

To explore how the total variance of our four climate variables is now re-partitioned in the derived principal components, we need to take a look a the eigenvalues. Recall, the eigenvalues are the variances explained by the principal components (one for each component). The square roots of the eigenvalues are stored in the prcomp object:

pca$sdev

## [1] 1.73331374 0.88945906 0.44527838 0.07882397

From this, we can easily calculate the variance explained by each component (the component variance divided by the total variance).

var_exp <- data.frame(pc = 1:4,
                      var_exp = pca$sdev^2 / sum(pca$sdev^2))

# add the variances cumulatively
var_exp$var_exp_cumsum <- cumsum(var_exp$var_exp)
var_exp

##   pc     var_exp var_exp_cumsum
## 1  1 0.751094132      0.7510941
## 2  2 0.197784356      0.9488785
## 3  3 0.049568208      0.9984467
## 4  4 0.001553304      1.0000000

The so called scree plot plots the component variances versus the component number. The idea is to look for an “elbow” which corresponds to the point after which the eigenvalues decrease more slowly.

par(mfrow=c(1,2))
plot(var_exp$pc, var_exp$var_exp, type="b", col=4,
     ylab="Fraction of explained variance", xlab="Principle Component")
plot(var_exp$pc, var_exp$var_exp_cumsum, type="b", col=6,
     ylab="Cummulative fraction variance", xlab="Principle Component")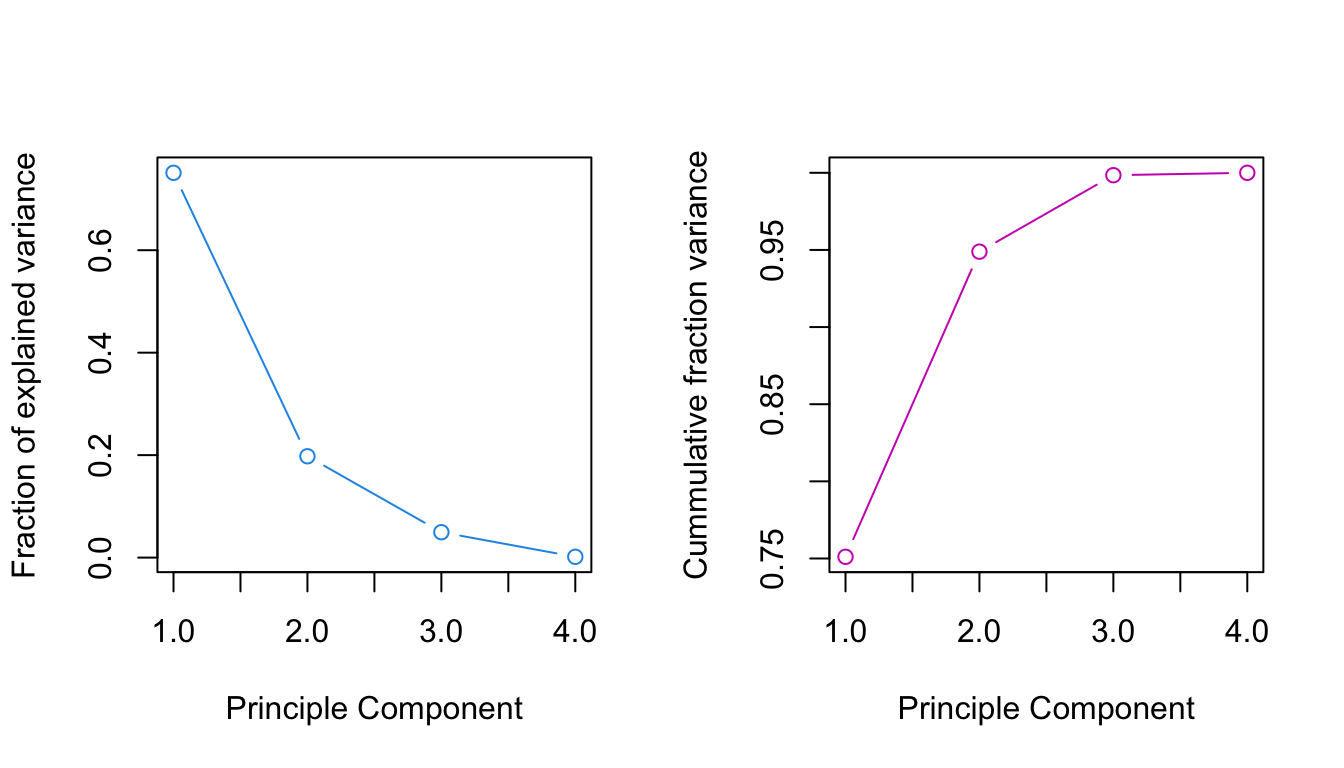

You are probably not surprised there is an easier way:

summary(pca)

## Importance of components:
##                           PC1    PC2     PC3     PC4
## Standard deviation     1.7333 0.8895 0.44528 0.07882
## Proportion of Variance 0.7511 0.1978 0.04957 0.00155
## Cumulative Proportion  0.7511 0.9489 0.99845 1.00000

The eigenvalues tell us: 75.1% of the variance is explained by PC1 alone, 19.8% by PC2, 5% by PC3, and only 0.16% by PC4. The cumulative proportion makes clear that 99.8% of the variance is captured by the first three components. Hence, we may discard PC4 without loosing much information.

Correlation analysis

Another way to interpret the meaning of the principal components is to explore the correlation between the PC scores and the original variables. Explore the scatter plot below and look at how PC1 is correlated with the orginal variables. Compare this to your observation of the rotation coefficients. You can do the same for PC2, PC3, and PC4.

df <- cbind(clim, pca_scores)
pairs(df[,1:7])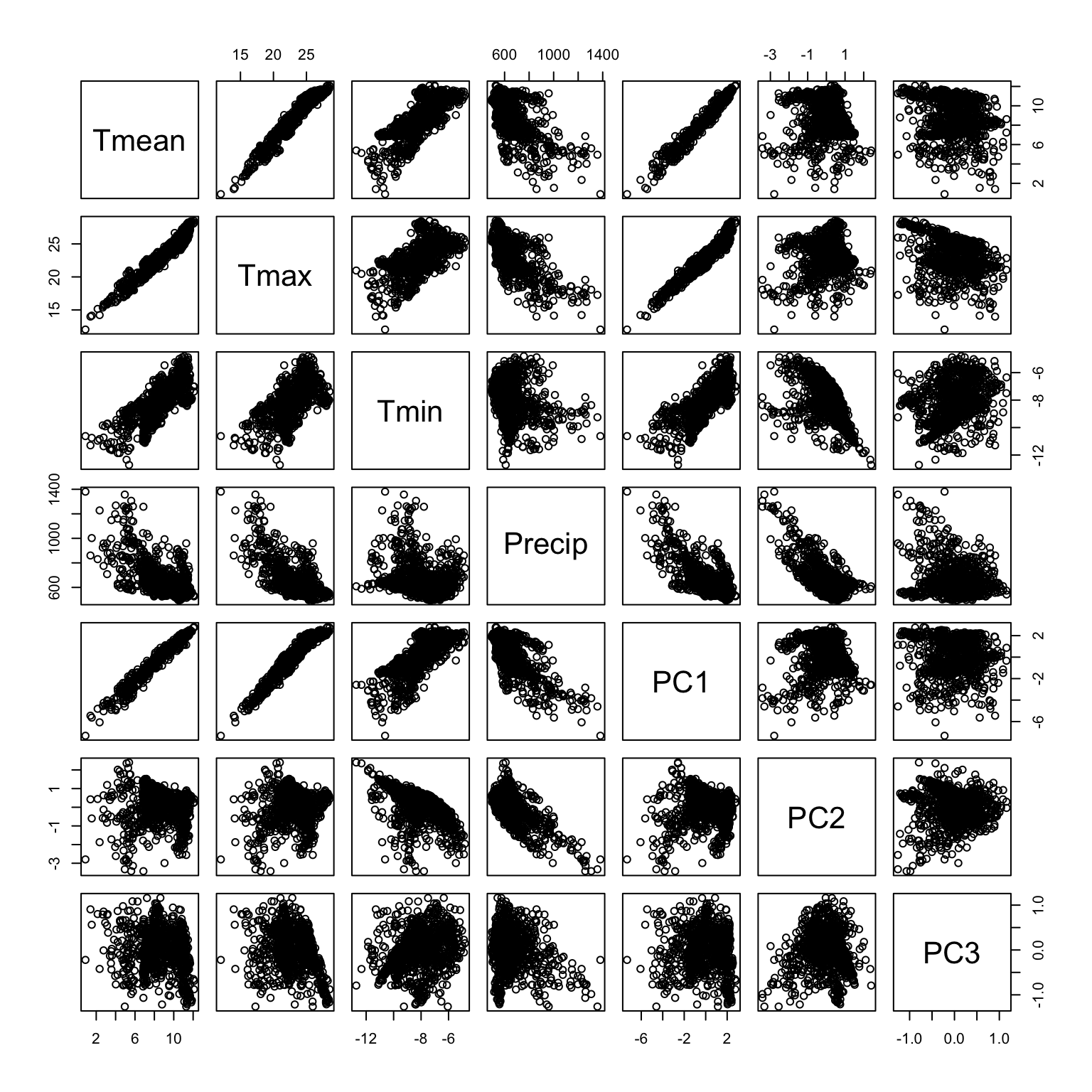

Biplot

The biplot shows the bioclim variables (in form of the rotation coefficients / loadings) and the observations (the PCA scores of our 10k samples) in one graphic. The variables are visualized as arrows from the plot origin, reflecting their direction and magnitude. Note, there are different versions of biplots out there also in different packages (e.g. PCAtools, ggbiplot).

biplot(pca)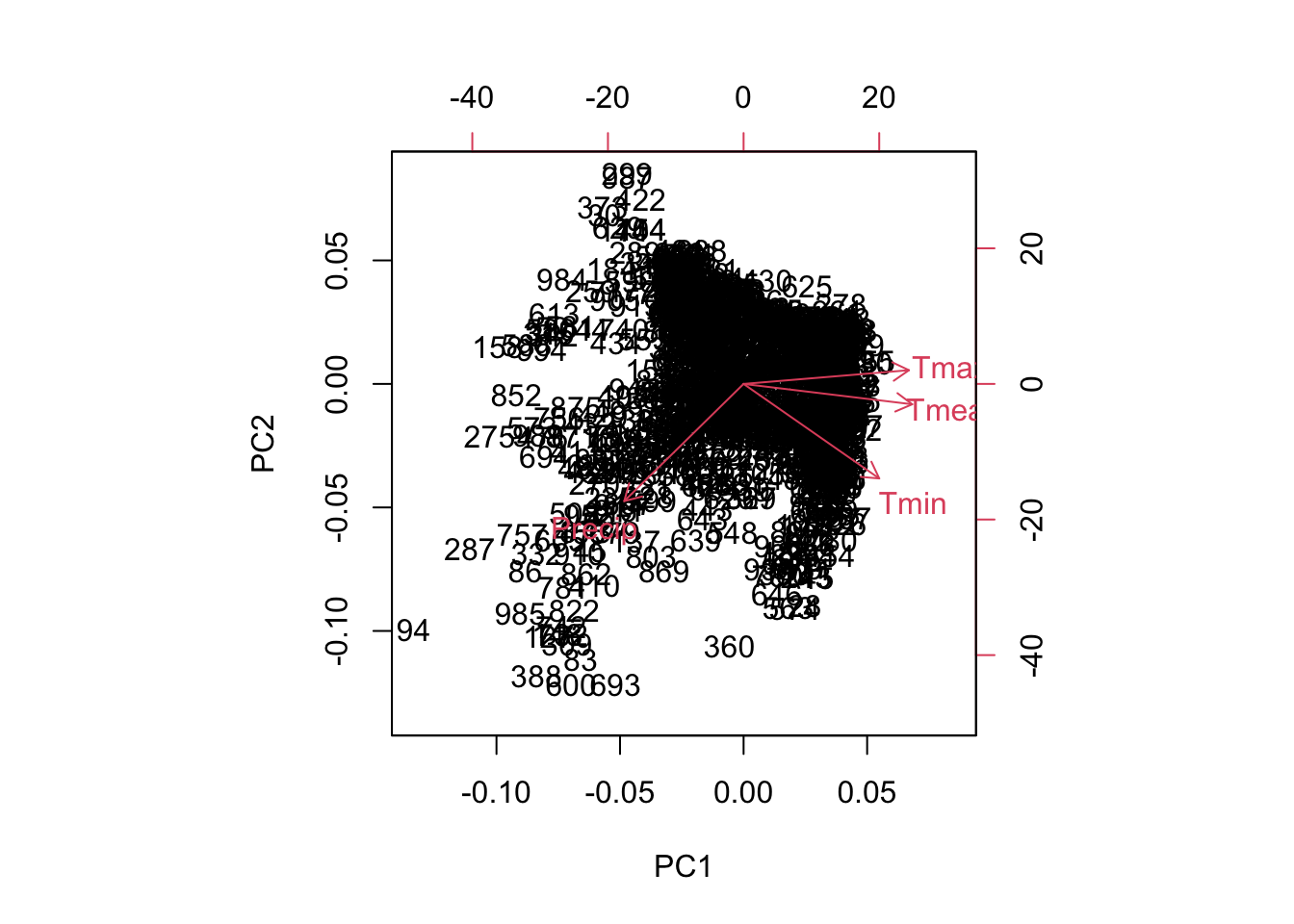

biplot(pca, choices=c(1,3))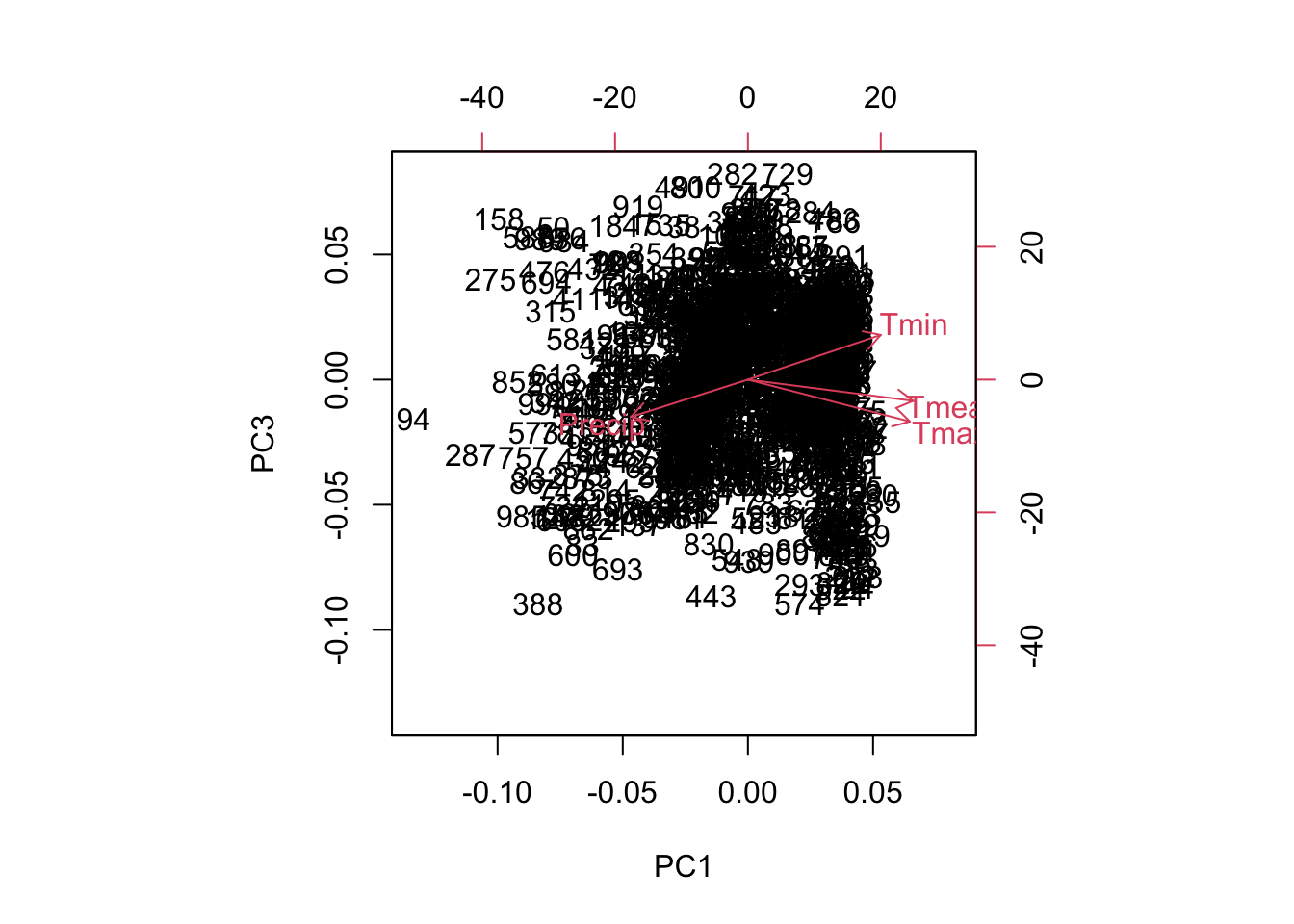

biplot(pca, choices=c(1,3), xlabs=rep('.', nrow(pca$x)))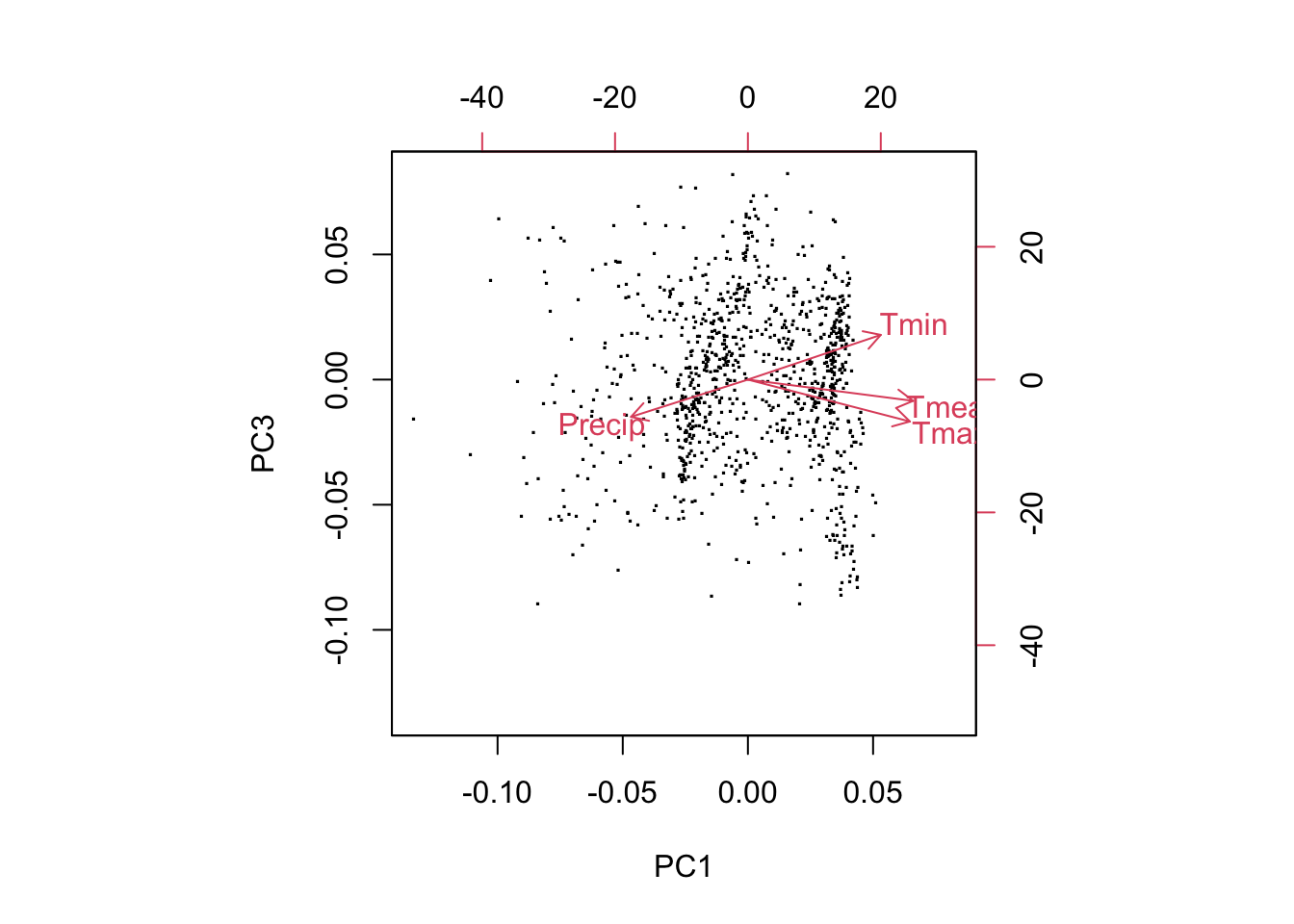

`prcomp` vs `princomp`

Description	prcomp()	princomp()
Decomposition method	svd()	eigen()
Standard deviations of the principal components	sdev	sdev
Matrix of variable loadings (columns are eigenvectors)	rotation	loadings
Variable means (means that were substracted)	center	center
Variable standard deviations (the scalings applied to each variable )	scale	scale
Coordinates of observations on the principal components	x	scores

Principal Component Analysis

Humboldt-Universität zu Berlin | Geography Department

Data

Fit PCA

Scores

Rotation coefficients

Eigenvalues

Correlation analysis

Biplot

`prcomp` vs `princomp`

Principal Component Analysis

Humboldt-Universität zu Berlin | Geography Department

Data

Fit PCA

Scores

Rotation coefficients

Eigenvalues

Correlation analysis

Biplot

prcomp vs princomp

`prcomp` vs `princomp`