- Learning goals
- Vegetation properties
- Vegetation Indices
- NDVI
- Assignment
6. Vegetation properties and indices
Learning goals
- Recap vegetation properties
- Get to know the Normalized Difference Vegetation Index (NDVI)
- Learn how to calculate the NDVI
- Understand the information content provided by the NDVI
Vegetation properties
Optical remote sensing enables the deduction of various vegetation-related characteristics, including biochemical properties (e.g., pigments, water content), structural properties (e.g., leaf area index (LAI), biomass) or process properties (e.g., light use efficiency (LUE)). The ability to deduce these characteristics depends on the ability of a sensor to resolve vegetation spectra. Hyperspectral sensors capture spectral information in hundreds of narrow and contiguous bands in the VIS, NIR and SWIR, and, thus, resolve subtle absorption features caused by specific vegetation constituents (e.g. anthocyanins, carotenoids, lignin, cellulose, proteins). In contrast, multispectral sensors capture spectral information in a few broad spectral bands and, thus, only resolve broader spectral features. Still, multispectral systems like Sentinel-2 have been demonstrated to be useful to derive valuable vegetation properties (e.g., LAI, chlorophyll).
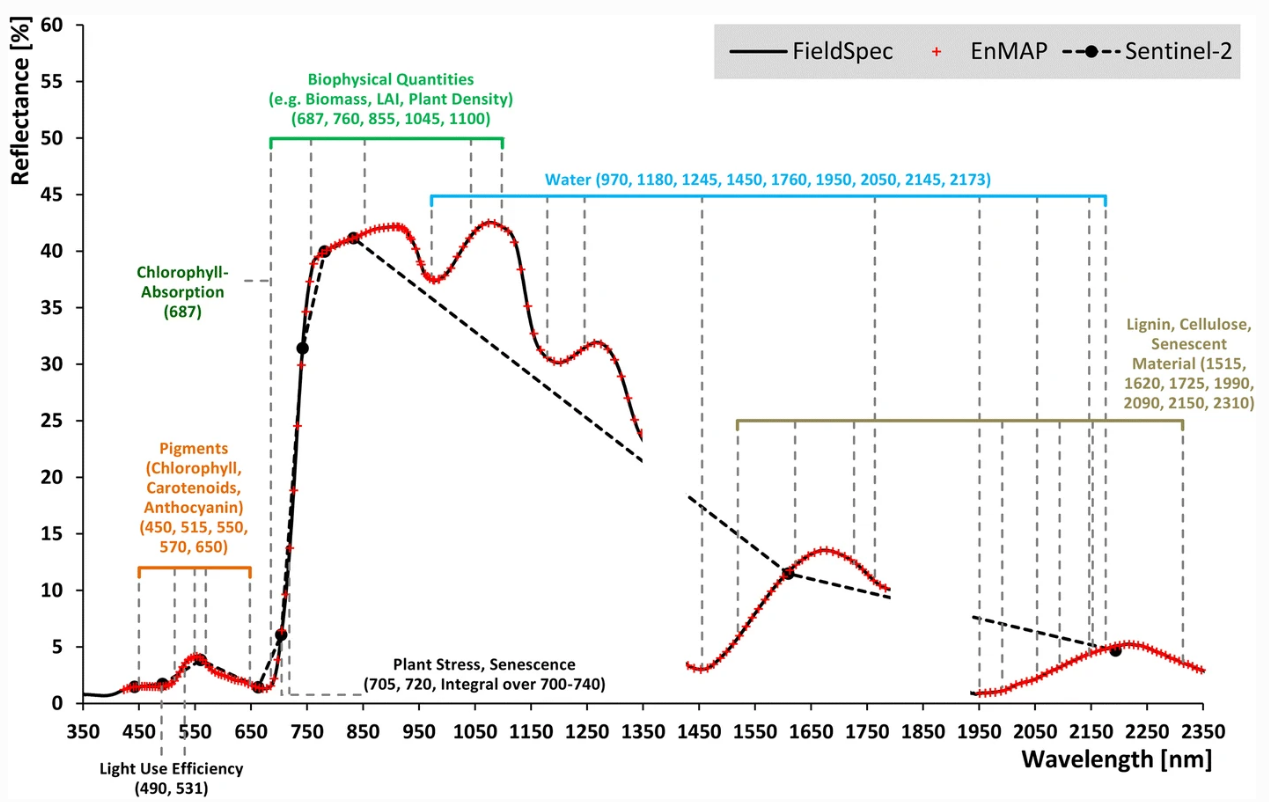
Vegetation Indices
A vegetation index (VI) represents a spectral transformation of two or more bands of spectral imagery into a singleband image. A VI is designed to enhance the vegetation signal with regard to different vegetation properties, while minimizing confounding factors such as soil background reflectance, directional, or atmospheric effects. There are many different VIs, including multispectral broadband indices as well as hyperspectral narrowband indices.
 Spectral
transformations
Spectral
transformations
Spectral indices have the advantage of being simple, but the disadvantage of disregarding information of the spectral feature space. Linear transformations, such as the Tasseled Cap Transformation, Principle Component Analysis (PCA) on the other hand make use of all information, but can be substantially more difficult to interpret thematically.
Data transformations apply some function f to transform an input x to an output f(x), motivated by emphasizing certain information in the data (vegetation, water, soil, etc.) and simultaneously reducing the dimensionality (e.g. 6-band to single-band image). In the remote sensing context, one such common linear transformation is called the Tasseled Cap Transformation (TC) which already comes with a prespecified focus on certain information regarding spectral brightness, greenness and wetness.
In case you are interested in exploring more spectral indices please see this exhaustive list of indices.NDVI
Most of the multispectral broadband indices make use of the inverse relationship between the lower reflectance in the red (through chlorophyll absorption) and higher reflectance in the near-infrared (through leaf structure) to provide a measure of greenness that can be indirectly related to biochemical or structural vegetation properties (e.g., chlorophyll content, LAI). The Normalized Difference Vegetation Index (NDVI) is one of the most commonly used broadband VIs:
NDVI=NIR−REDNIR+RED
The NDVI calculation results in an singleband grayscale image, with a potential range of NDVI values between -1 and 1. For all possible input combinations of RED and NIR we observe the following NDVI values:
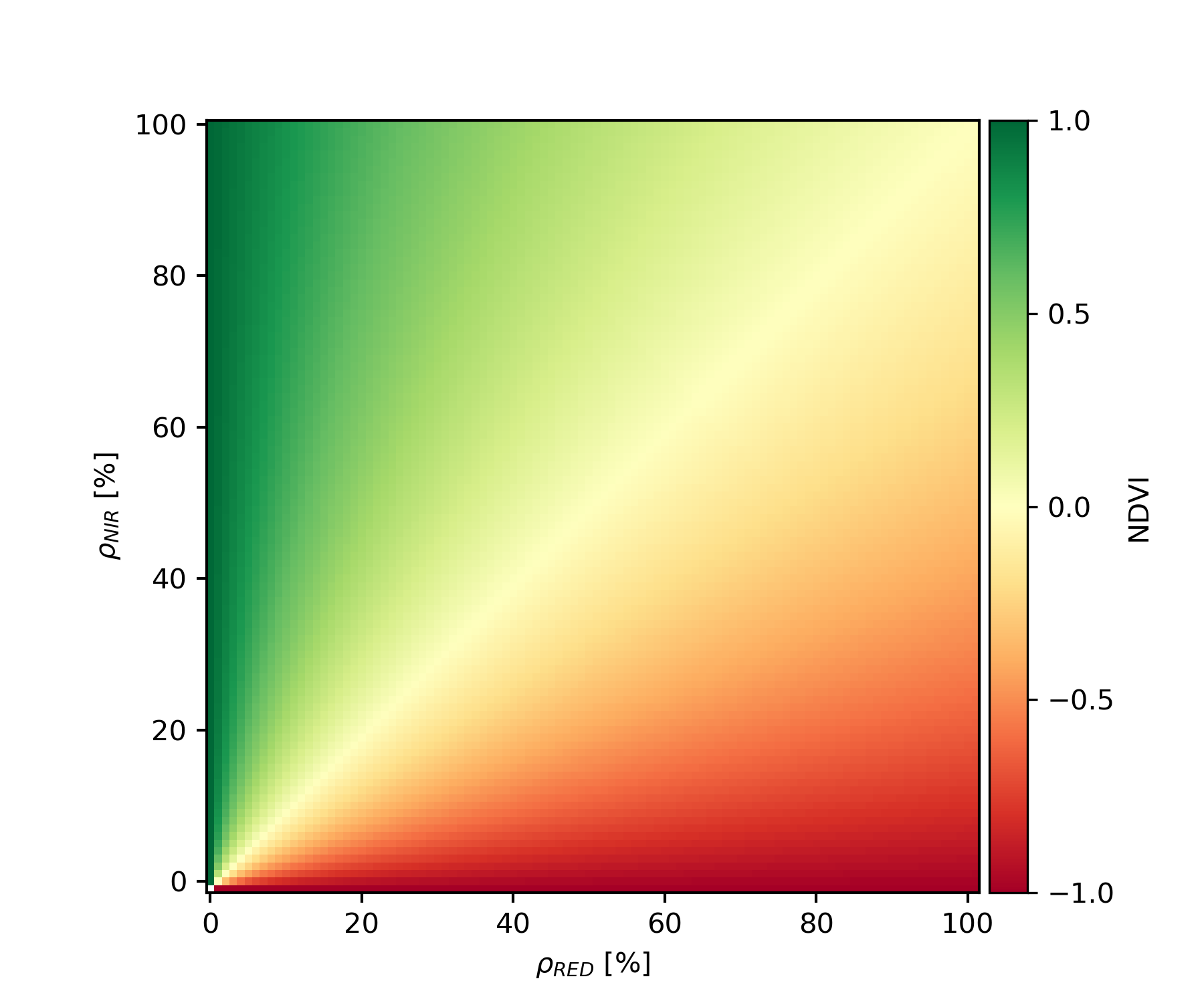
The NDVI is a great proxy for photosynthetic activity, leaf vitality, vegetation density and canopy structure. It is, however, not a biophysical variable. Nevertheless, because of its relation to vegetation density and structure, the NDVI may be used to estimate biophysical parameters such as the Leaf Area Index (LAI).
Take a look at the NDVI formula above. Think about the (general) spectral behaviour of 1) water, 2) soil, and 3) vegetation (take a look at last week’s plots if needed). Roughly which NDVI values would you expect to observe for these surface types?

Next, we will take a look at how to calculate the NDVI in R. We will see there are many options, but first we consider the simplest when dealing with only one image:
Exercise 2
Start by reading in your Sentinel-2 image from
the last sessions (the one that is scaled and reprojected) into R. In
Session 3 you applied simple arithemtic to scale your data. Along these
lines, we can now also calculate the NDVI by simply treating the correct
bands of the SpatRaster as inputs to our formula. An
example:
# two hypothetical measurements in the red and nir
red <- 0.045 # 4.5%
nir <- 0.382 # 38.2%
ndvi <- (nir-red)/(nir+red)
print(paste0("NDVI: ", round(ndvi, 3)))## [1] "NDVI: 0.789"In the above example we simulate the calculation on a single pixel. Now calculate the NDVI for the entire image:
# ...
# print and plot resulting single-band NDVI
print(ndvi)
plot(ndvi)img_s2 # our 6-band Sentinel-2 image
# option 1
red <- img_s2$RED # or index: img_s2[[3]]
nir <- img_s2$NIR # or index: img_s2[[4]]
ndvi <- (nir-red)/(nir+red)
# option 2
ndvi <- (img_s2$NIR-img_s2$RED)/(img_s2$NIR+img_s2$RED)
# print and plot resulting single-band NDVI
print(ndvi)
plot(ndvi)Remember functions? Of course! - You work with them all the time,
like rast(), plot(), … But we can also create
our own functions in R: User-defined functions.
Calculations such as the NDVI are a good example for tasks we do repeatedly for different images. So let’s see how we can create a function which allows us to calculate the NDVI given an input image.
 User-defined
functions in R
User-defined
functions in R
User-specified functions come in handy whenever a certain chain of instructions need to be repeated or generalized. A function is a set of statements organized together to perform a specific task. Using functions greatly enhances code structure as it improves the clarity and readability of your script.
Function arguments are provided in round () brackets
following the function class. Between {}
stands the function body which contains the collection of statements
which should be executed when calling the function. At the end there is
usually an output, specified within return().
Let’s create a simple “coin-flip” function:
# coin-flip function -
coin_flip <- function(n_flips=1) {
flip_result <- sample(c("Heads", "Tails"), size=n_flips, replace=TRUE)
return(print(flip_result))
}
# single coin flip
coin_flip()## [1] "Heads"# 5 coin_flips
coin_flip(5)## [1] "Heads" "Tails" "Tails" "Heads" "Tails"Let’s implement our own NDVI function we can use in the future.
Exercise 3
Create a function called calc_ndvi
which expects two arguments as inputs: the red and nir single-band
images, and returns a single-band NDVI image. After checking the result
for correctedness, export it to disc or take a look at the optional
exercise below.
calc_ndvi <- function(red, nir) {
}Advanced (optional): Expand the functionality of
calc_ndvi to provide a filename as function argument which
- if provided - saves the resulting NDVI to disc. Ideally
scaled and in 16bit signed (+ and -) integer (INT2S)
calc_ndvi <- function(red, nir, filename=NULL) {
# your ndvi calculation from above
# ...
# check if filename is not equal (!) to NULL; i.e.
# a filename was provided to the function
if (!is.null(filename)) {
# scale
# export image to disc
}
# your "return" from above
# ...
}calc_ndvi <- function(red, nir) {
# your ndvi calculation from above
ndvi <- (nir-red)/(nir+red)
names(ndvi) <- "NDVI"
return(ndvi)
}
calc_ndvi <- function(red, nir, filename=NULL) {
# your ndvi calculation from above
ndvi <- (nir-red)/(nir+red)
names(ndvi) <- "NDVI"
# check if filename is not equal (!) to NULL; i.e.
# a filename was provided to the function
if (!is.null(filename)) {
# scale
ndvi <- ndvi * 10000 # prepare for integer export
# export image to disc
writeRaster(ndvi, filename=filename, datatype="INT2S")
}
# return ndvi as SpatRast object
return(ndvi)
}Assignment
The senate of Berlin would like to have a first short assessment of the amount and condition of the urban vegetation within city borders. Specifically, the senate would like to get a first idea how much of the area is covered by vegetation. Based on the NDVI, they want you to assign to each pixel if it represents vegetation cover, or not. For instance, you could say that everything above a NDVI of 0.85 represents full vegetation cover, while everything below 0.85 does not.
Greenness of Berlin: Conceptual implications
Before you get started, you explain to the senate that finding a NDVI threshold which separates vegetation from non-vegetation is not a straightforward task. Think about the data you are using, and recap the theory on the NDVI from the lecture to list at least 3 points that complicate finding a universal, exact threshold.
Greenness of Berlin: Land cover - NDVI relationship
Display the NDVI as grayscale image and the Sentinel-2 image as true-colour composite in QGIS. Simultaneously, have the NDVI image ready-for-analyses in R.
First, use the Identify cursor location values functionality and the histogramm in QGIS to
answer the following questions:
- What is the range of NDVI values for the entire image (min, max), and which land cover types are likely located at these extrema?
- What are typical NDVI values for 1) built-up, 2) vegetation (grassland, deciduous, evergreen, cropland), and 3) water? (Tipp: Visit some of the land cover points you sampled in Session 5 and visually intepret your NDVI image in QGIS to get a rough estimate how these 3 surfaces behave) You could also extract and plot the NDVI values for these points in R.
Greenness of Berlin: A first map
The senate would like you to create a vegetation map based the area covered by leafes (the Leaf-Area-Index, LAI) approximated via its relationship to the NDVI (Lecture slide 14). The map should label every pixel as vegetation where at least 3 square meters are covered by leafes (LAI = 3). This map hence focuses on rather densely covered pixels. To identify the NDVI threshold for creating this map, take a look at the graph on lecture slide 14, showing the general LAI-NDVI relationship.
- Why is finding such a threshold based on this graph difficult and not ideal?
- Could we attempt to separate even denser canopies (LAI > 3) from lower density canopies?
Use a best estimate of the NDVI threshold (e.g. mean in plot) to
approximately separate pixels with LAI > 3 and LAI <= 3. Once you
have your threshold, you can use the following code to create a simple
binary map containing 1 for vegetation and 0
for non-vegetation:
# 'ndvi' is your NDVI image
# 'ndvi_threshold' is your chosen value to separate the cover
ndvi_threshold <-
# Use "greater than" > to check for every pixel if the value is greater than
# the ndvi threshold; If true, "vegetation" will contain 1, if false, "vegetation"
# will contain 0
vegetation <- ndvi > ndvi_threshold
plot(vegetation)
# write your map to disc
writeRaster()Take a quick look at your result in QGIS. Compare the result to Google VHR imagery and your Sentinel-2 image. Are you satisfied with the product? Does the map allow you to get a good apprximation of vegetation presence within Berlin?
Copyright © 2023 Humboldt-Universität zu Berlin. Department of Geography.